Examining quantum gravity's effects on gravitational rainbows

Abstract

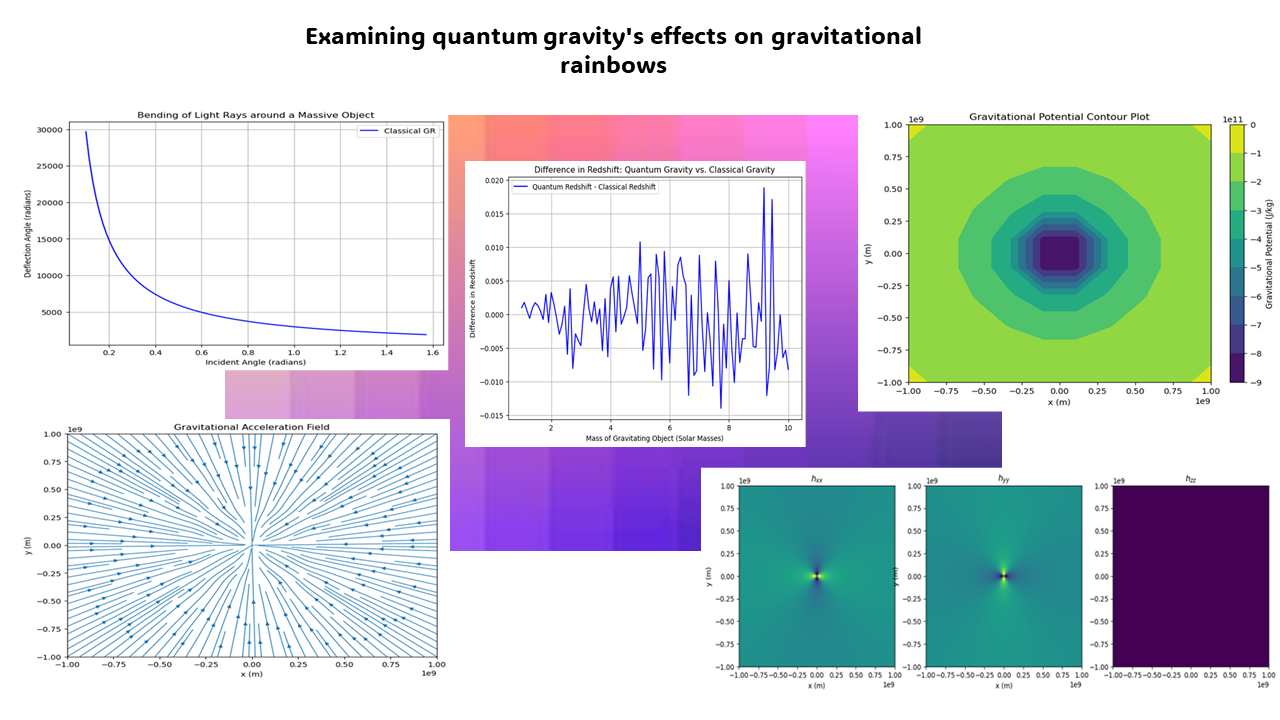
This paper delves into the fundamental implications of quantum gravity on gravitational rainbows, an intriguing phenomenon resulting from the interaction between quantum mechanics and gravity. We explore the theoretical underpinnings of quantum gravity and how they affect light bending around enormous objects, providing insight into the phenomenon known as gravitational rainbows. We investigate the complex interplay between quantum gravity and gravitational events by thoroughly analyzing theoretical models, experimental findings, and computer simulations, providing insights into the essence of the cosmos. The results show that according to the basic theories of light propagation, light moves along the x-axis at a constant speed based on observing a straight-line route between the affine parameters and the x-coordinate. The analysis of shifting gravitational potentials reveals significant influences on the routes taken by light beams traveling through gravitational fields. The impact of quantum gravitational effects is emphasized by the gravitational potential spreading outward, reaching magnitudes of 10 × 10¹¹ and decreasing towards zero outward. Moreover, the gravitational disturbance distribution is closest to the coordinate system center, with minor perturbations in the z-direction, especially in ℎxx and ℎyy. This distribution highlights how gravitational influences vary throughout space. Finally, the analysis shows that, due to a decrease in the impact parameter, the deflection angle of light increases as the angle of incidence lowers. Additionally, the deflection angle is directly influenced by the mass of the deflecting objects, suggesting a proportionate link between mass and deflection. These findings advance our knowledge of gravitational events in astrophysical and cosmological contexts and offer insight into how light behaves in gravitational fields.