Mapping solar variability of equatorial sunspots and plasma flows

Authors

DOI:

https://doi.org/10.14295/bjs.v3i9.638

Keywords:

sunspot numbers, solar magnetic field, plasma flows, solar differential rotation, meridional circulation, magnetic induction equation

Abstract

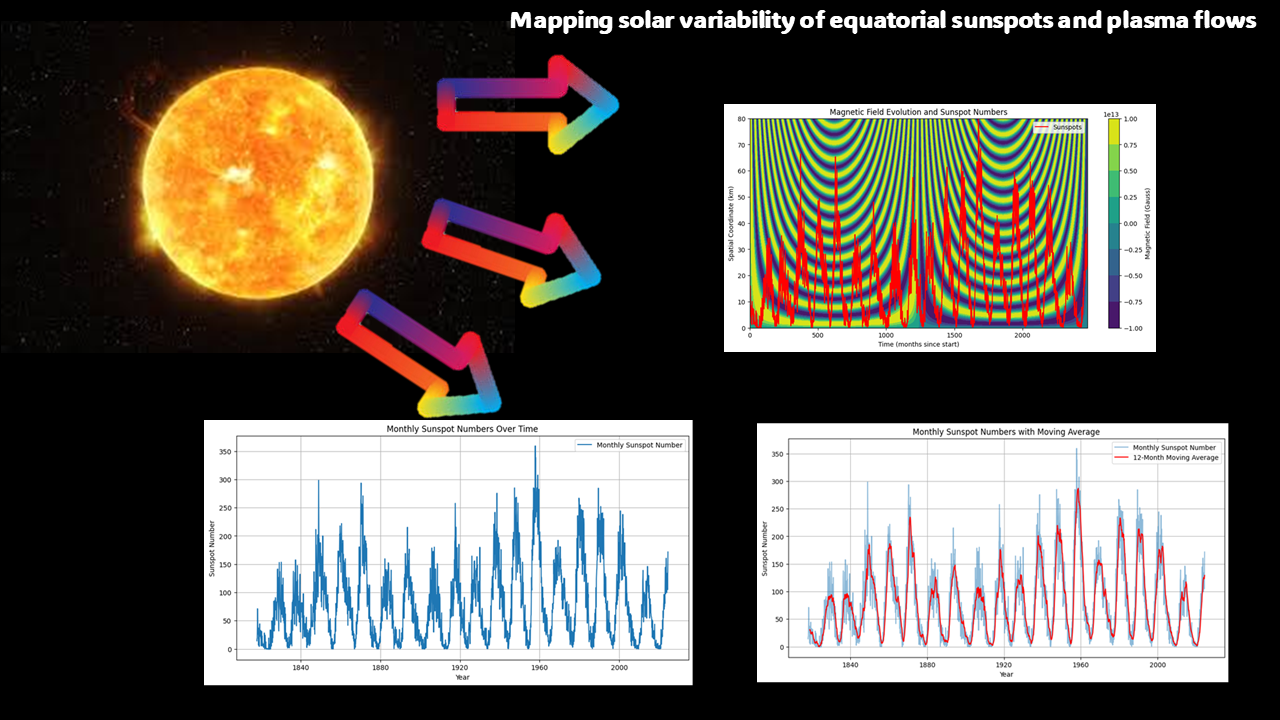
This study investigated the variability of equatorial sunspots and plasma flows, focusing on the detailed dynamics of solar activity revealed by sunspot data analysis and magnetic field evolution. The goals were to investigate the relationship between sunspot numbers with differential rotation, meridional circulation, and magnetic induction using observational data and theoretical models. The methods included studying historical sunspot data from 1700 to the present and using time series decomposition to find trends, seasonality, and residuals. The evolution of the solar magnetic field was predicted using the magnetic induction equation, which considers plasma flow and magnetic diffusion effects. The real sunspot data were combined with the simulated magnetic field data to investigate their relationship over time. Contour maps were created to illustrate the spatiotemporal evolution of the magnetic field, and correlation studies were used to quantify the correlations between sunspot numbers and key solar dynamics characteristics. Key studies show that the Sun rotates differentially, with latitudinal zones rotating at differing angular velocities, influencing sunspot generation. A strong connection (0.8192) between the sunspot numbers and meridional velocity demonstrates the influence of large-scale plasma flows on sunspot activity. Despite this, the monthly averaged magnetic field strength and sunspot numbers exhibited a minor correlation (0.004507), showing that solar activity is affected by independent underlying processes or phases. Magnetic field evolution contour maps show differences from 1x1013 to 2x1013 Gauss at different spatial (40 km to 80 km) and temporal scales (from start to the present in months). This evolution is governed by the magnetic induction equation, which includes the effects of plasma flow and magnetic diffusion. The paper also emphasizes the alpha effect's significance in producing poloidal magnetic fields from toroidal fields via turbulent convection, which is essential to the solar dynamo mechanism. In conclusion, this study provides a comprehensive analysis of equatorial sunspots and plasma flows, offering insights into the solar cycle and laying the groundwork for future research in solar and space weather prediction.

References

Brun, A. S., & Toomre, J. (2002). Turbulent convection under the influence of rotation: Sustaining a strong differential rotation. The Astrophysical Journal, 570(2), 865-873. https://doi.org/10.1086/339228 DOI: https://doi.org/10.1086/339228

Charbonneau, P. (2010). Solar dynamo theory. Living Reviews in Solar Physics, 7(3), 3-13. https://doi.org/10.12942/lrsp-2010-3 DOI: https://doi.org/10.12942/lrsp-2010-3

Dikpati, M., & Charbonneau, P. (1999). A babcock-leighton flux transport dynamo with solar-like differential rotation. The Astrophysical Journal, 518(1), 508-520. https://doi.org/10.1086/307269 DOI: https://doi.org/10.1086/307269

Fan, Y. (2009). Magnetic fields in the solar convection zone. Living Reviews in Solar Physics, 6(1), 4-13. https://doi.org/10.12942/lrsp-2004-1 DOI: https://doi.org/10.12942/lrsp-2009-4

Gizon, L., & Birch, A. C. (2005). Local helioseismology. Living Reviews in Solar Physics, 2(6), 6-14. https://doi.org/10.12942/lrsp-2005-6 DOI: https://doi.org/10.12942/lrsp-2005-6

Hathaway, D. H., & Rightmire, L. (2010). Variations in the sun’s meridional flow over a solar cicle. Science, 327(5971), 1350-1352. https://doi.org/10.1126/science.1181990 DOI: https://doi.org/10.1126/science.1181990

Hathaway, D. H. (2015). The Solar Cycle. Living Reviews in Solar Physics, 12(1), 4-10. https://doi.org/10.1007/lrsp-2015-4 DOI: https://doi.org/10.1007/lrsp-2015-4

Imada, S., Matoba, K., Fujiyama, M., & Iijima, H. (2020). Solar cycle-related variation in solar differential rotation and meridional flow in solar cycle 24. Earth, Planets and Space, 72. https://doi.org/10.1186/s40623-020-01314-y DOI: https://doi.org/10.1186/s40623-020-01314-y

Kitiashvili, I. N., et al., (2019). The solar flare prediction using a three-dimensional topological magnetic field model. The Astrophysical Journal, 885(1), 51-63.

Miesch, M. S. (2005). Large-scale dynamics of the convection zone and tachocline. Living Reviews in Solar Physics, 2(1), 1-12. https://doi.org/10.12942/lrsp-2005-1 DOI: https://doi.org/10.12942/lrsp-2005-1

Moffatt, H. K. (1978). Magnetic field generation in electrically conducting fluids. Cambridge University Press.

Montgomery, D. C., Jennings, C. L., & Kulahci, M. (2008). Introduction to time series analysis and forecasting. John Wiley & Sons. Inc. Hoboken New Jersey, Second Edition, Wiley.

Norton, A., Hoew, R., Upton, L., & Usoskin, I. (2023). Solar cycle observation. Space Science Reviews, 219. https://doi.org/10.1007/s11214-023-01008-3 DOI: https://doi.org/10.1007/s11214-023-01008-3

Ossendrijver, M. (2003). The solar dynamo. The Astronomy and Astrophysics Review, 11(4), 287-367. http://dx.doi.org/10.1007/s00159-003-0019-3 DOI: https://doi.org/10.1007/s00159-003-0019-3

Parker, E. N. (1979). Cosmical magnetic fields: Their origin and activity. Oxford Classic Texts in the physical sciences, Oxford University Press, United Kingdom.

Priest, E. R., & Forbes, T. G. (2002). Magnetic reconnection: MHD theory and applications. Cambridge University Press.

Priest, E. (2014). Magnetohydrodynamics of the Sun. Cambridge University Press, New York, NY, USA. DOI: https://doi.org/10.1017/CBO9781139020732

Rempel, M. (2005). Solar differential rotation and meridional flow: The role of a subadiabatic tachocline for the Taylor–Proudman balance. The Astrophysical Journal, 622(2), 13-20. https://doi.org/10.1086/428282 DOI: https://doi.org/10.1086/428282

Riley, P. (2017). On the probability distribution function of solar flare occurrences. The Astrophysical Journal, 835(1), 41-53.

Schrijver, C. J., & Van Ballegooijen, T. (1997). The solar dynamo. Astrophysics and Space Science Library, 219, 107-116.

Solanki, S. K., & Fligge, M. (2003). Sunspots: An overview. Astronomy and Astrophysics Review, 11(3-4), 153-286. https://doi.org/10.1007/s00159-003-0018-4 DOI: https://doi.org/10.1007/s00159-003-0018-4

Stenflo, J. O. (2013). Solar magnetic fields as revealed by stokes polarimetry. Astronomy & Astrophysics Review, 21(1), 66-74. https://doi.org/10.1007/s00159-013-0066-3 DOI: https://doi.org/10.1007/s00159-013-0066-3

Downloads

Published

2024-07-20

How to Cite

Goshu, B. S. (2024). Mapping solar variability of equatorial sunspots and plasma flows. Brazilian Journal of Science, 3(9), 49–64. https://doi.org/10.14295/bjs.v3i9.638

Issue

Vol. 3 No. 9 (2024): Brazilian Journal of Science

Section

Exact Sciences

License

Copyright (c) 2024 Belay Sitotaw Goshu

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

 

Authors who publish with this journal agree to the following terms:

1) Authors retain copyright and grant the journal right of first publication with the work simultaneously licensed under a Creative Commons Attribution License that allows others to share the work with an acknowledgement of the work's authorship and initial publication in this journal.

2) Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the journal's published version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgement of its initial publication in this journal.

3) Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work.